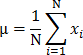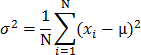Beschrijvende statistiek
Met de beschrijvende statistieken worden getallen bedoeld die een (grote) gegevensverzameling karakteriseren. Deze getallen vormen een maat voor de grootte, het centrum, en de spreiding van de verzameling. Door alleen naar deze getallen te kijken kun je snel zien of gegevens die je hebt verzameld over twee variabelen op elkaar lijken of juist verschillen.
Grootte
De grootte van een gegevensverzameling wordt gemeten als het aantal elementen in die verzameling. Vaak spreekt men van "het aantal waarnemingen". Dit aantal wordt aangegeven met de letter N (van het Engelse number).
Centrum
Om het centrum van een gegevensverzameling te bepalen worden drie verschillende indicatoren gebruikt:
- Voor numerieke waarden kan het gemiddelde μ worden berekend als de som van alle waarden gedeeld door hun aantal N. Als formule geschreven:
- De mediaan is de waarde van het middelste element in de gegevensverzameling wanneer deze in oplopende waarde is geordend. Als de gegevensverzameling een even aantal elementen heeft, en er dus geen middelste element is, wordt voor de mediaan het gemiddelde van de elementen N/2 en N/2 + 1 genomen.
- De modus is de waarde die het vaakst voorkomt in de gegevensverzameling.
Spreiding
De spreiding van een gegevensverzameling wordt beschreven door vier getallen:
- Het minimum en het maximum, d.w.z. de laagste en de hoogste waarde in de verzameling.
- De variantie σ2, berekend als de som (over alle waarden x in de verzameling) van het kwadraat van de afwijking van x t.o.v. het gemiddelde μ. Als formule geschreven:
- De standaarddeviatie (of standaardafwijking) σ, gedefinieerd als de vierkantswortel uit de variantie σ2. Daarmee heeft σ dezelfde dimensie als de grootheid waarvan de spreiding bepaald wordt, en kan deze bijvoorbeeld in een diagram langs dezelfde as gebruikt worden. Zie hiervoor bijvoorbeeld deze figuur, waarin de normale verdeling gegeven is met gemiddelde μ en standaardafwijking σ.
Kwartielen en Percentielen
Om een gegevensverzameling te karakteriseren worden soms ook kwartielen of percentielen als indicatoren gebruikt. Als je een gegevensverzameling hebt gesorteerd in oplopende volgorde van waarden is het eerste kwartiel de waarde van het ((N+1)/4)e element, het tweede kwartiel de waarde van het ((N+1)/2)e element, en het derde kwartiel de waarde van het (3·(N+1)/4)e element. Evenzo is het pe percentiel de waarde van het (p·N/100)e element.
Dus:
- 25e percentiel = eerste kwartiel
- 50e percentiel = tweede kwartiel = mediaan
- 75e percentiel = derde kwartiel
Zie ook
- Aggregatie
- Oefeningen:Beschrijvende statistiek
- De kennisclip over het maken van een histogram op YouTube en het bijbehorende model in Excel.
- De Wikipedia-artikelen over scheefheid en kurtosis